While analyzing a performance issue with a 63-table join query (you gotta love Siebel) I came accross a little optimizer oddity. Looking at a 600MB optimizer trace was fun, though 😉
The problem boiled down to this:
------------------------------------------------------------------------------------------
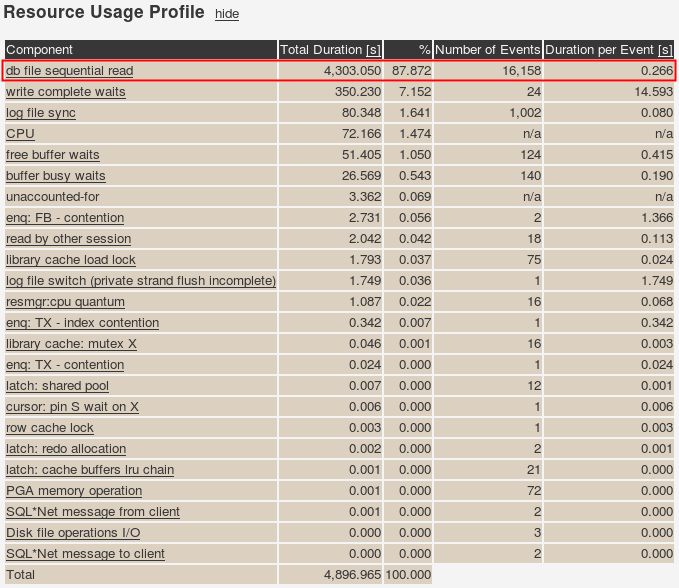
| Id | Operation | Name | Rows | Bytes | Cost (%CPU)| Time |
------------------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 83 | 6225 | 10 (0)| 00:00:01 |
| 1 | NESTED LOOPS OUTER | | 83 | 6225 | 10 (0)| 00:00:01 |
|* 2 | TABLE ACCESS STORAGE FULL | T1 | 2 | 20 | 9 (0)| 00:00:01 |
| 3 | TABLE ACCESS BY INDEX ROWID| T2 | 41 | 2665 | 1 (0)| 00:00:01 |
|* 4 | INDEX UNIQUE SCAN | T2_IDX_01 | 1 | | 0 (0)| 00:00:01 |
------------------------------------------------------------------------------------------
Would you expect the cardinality estimate for table access on T2 (plan Id 3) to be 41?
I certainly wouldn’t. It’s doing an INDEX UNIQUE SCAN on index T2_IDX_01 (plan Id 4) and according to the cardinality estimate on T2 (plan Id 2) it will do that INDEX UNIQUE SCAN two times.
Why does the optimizer think it will get 41 rows per given ID value in the index while obviously a UNIQUE INDEX SCAN can only return 0 or 1 ROWID?
From the large Siebel query I managed to deduce a simple test case:
create table t1 (
id number(10) not null
, id2 number(10) not null
, id3 number(10)
, constraint t1_pk primary key (id)
using index (create unique index t1_idx_01 on t1 (id))
);
create table t2 (
id number(10)
, text varchar2(100)
, constraint t2_pk primary key (id)
using index (create unique index t2_idx_01 on t2 (id))
);
Only table T1 is populated with data. Column ID3 will be 50% NULL values, the other 50% will be “1”.
insert into t1 (id, id2, id3)
select
rownum id
, rownum id2
, decode(mod(rownum, 2), 0, null, 1) id3
from dual connect by level <= 10000
;
commit;
-- gather stats on T1 and related indexes without histograms
exec dbms_stats.gather_table_stats(user, 'T1', cascade => true, method_opt => 'FOR ALL COLUMNS SIZE 1')
And that’s the query which produced above execution plan:
select *
from t1
, t2
where t1.id2 in (10, 20)
and t1.id3 = t2.id(+)
;
Perhaps you noticed that I didn’t gather statistics for table T2, which was exactly the sitution I had in the Siebel database. Several tables involved in the 63-table join did not have statistics on them.
In case you’re wondering, according to Oracle’s Siebel “best practice” you’re not supposed to have statistics on tables with less than 15 rows in them (see Oracle’s script coe_siebel_stats.sql v11.4.4.6).
Now, back to the orginal question: How does Oracle come up with 41?
First, for any table that does not have statistics Oracle seems to assume a cardinality of 82. I don’t know where that magic number comes from. Maybe it simply takes 1% of 8192, the default database block size.
The extract from optimizer trace shows table T2 is not analyzed and contains 82 rows:
BASE STATISTICAL INFORMATION
***********************
Table Stats::
Table: T2 Alias: T2 (NOT ANALYZED)
#Rows: 82 SSZ: 0 LGR: 0 #Blks: 1 AvgRowLen: 100.00 NEB: 0 ChainCnt: 0.00 SPC: 0 RFL: 0 RNF: 0 CBK: 0 CHR: 0 KQDFLG: 0
#IMCUs: 0 IMCRowCnt: 0 IMCJournalRowCnt: 0 #IMCBlocks: 0 IMCQuotient: 0.000000
Column (#1): ID(NUMBER) NO STATISTICS (using defaults)
AvgLen: 13 NDV: 3 Nulls: 0 Density: 0.390244
...
SINGLE TABLE ACCESS PATH
...
Table: T2 Alias: T2
Card: Original: 82.000000 Rounded: 82 Computed: 82.000000 Non Adjusted: 82.000000
Also, the optimizer guesses the NDV(3) and number of nulls(0) for the ID column of table T2.
… if you think it simply divides 82 by 2, read on 🙂 …
Secondly, after studying different data patterns I think this is what happens.
Because of above outlined assumptions the adjusted selectivty for T2 will always be 1 in the join selectivity calculation.
And, since we have a low NDV on T1.ID3 we end up with a gross misestimate for the join selectivity.
join-sel =
((num_rows(t1) - num_nulls(t1.id3) / num_rows(t1)) *
((num_rows(t2) - num_nulls(t2.id) / num_rows(t2)) /
greater(num_distinct(t1.id3), num_distinct(t2.id))
join-sel =
((10000 - 5000 / 10000) *
((82 - 0 / 82) /
greater(1, 3)
= 0.16666666666666666666666666666667
From the optimzer trace we see that the join selectivity of 0.500000 does not exactly match our calculation. Interestingly, the optimizer seems to ignore the guessed NDV of 3 for T2.ID and instead use the NDV from T1.ID3, which would give you 0.5.
Outer Join Card: 83.000000 = max ( outer (2.000000),(outer (2.000000) * inner (82.000000) * sel (0.500000)))
So here it is, we’ve got our number 41: (82.000000) * sel (0.500000)
Note, the table access cardinality (plan Id 3) is based on the join selectivity which doesn’t account for the in-list predicate on T1, as one would expect. The in-list is accounted for in the filtered table cardinality of table T1 and so is reflected in the join cardinality (plan Id 1).
Lastly, the cardinality estimate for plan Id 3 (TABLE ACCESS BY INDEX ROWID) is independently calculated from plan Id 4 (INDEX UNIQUE SCAN). I think there should be a sanity check to adjust the estimate for the table access to T2 (plan Id 3) when the row source is fed by an INDEX UNIQUE SCAN.
Here’s another example:
insert into t1 (id, id2, id3)
select
rownum id
, rownum id2
, decode(mod(rownum, 4), 0, null, dbms_random.value(1, 6)) id3
from dual connect by level <= 10000
;
commit;
-- gather stats on T1 without histograms
exec dbms_stats.gather_table_stats(user, 'T1', cascade => true, method_opt => 'FOR ALL COLUMNS SIZE 1')
This time, column ID3 contains 25% NULL values, the other 75% are evenly distributed between “1” and “6”.
SQL> select column_name, histogram, num_distinct, density, num_nulls from dba_tab_columns where table_name = 'T1' order by column_name;
COLUMN_NAME HISTOGRAM NUM_DISTINCT DENSITY NUM_NULLS
------------------------------ --------------- ------------ ---------- ----------
ID NONE 10000 .0001 0
ID2 NONE 10000 .0001 0
ID3 NONE 6 .166666667 2500
So, according to above formulae & data it would go like this:
join-sel =
((10000 - 25000 / 10000) *
((82 - 0 / 82) /
greater(6, 3)
= 0.125
card = round(82 * 0.125) = 10
Again, the optimizer trace confirms the calculation, this time it’s spon-on because it again uses the NDV from T1.ID3 (which is greater than 3 anyway):
Outer Join Card: 21.000000 = max ( outer (2.000000),(outer (2.000000) * inner (82.000000) * sel (0.125000)))
------------------------------------------------------------------------------------------
| Id | Operation | Name | Rows | Bytes | Cost (%CPU)| Time |
------------------------------------------------------------------------------------------
| 0 | SELECT STATEMENT | | 21 | 1596 | 10 (0)| 00:00:01 |
| 1 | NESTED LOOPS OUTER | | 21 | 1596 | 10 (0)| 00:00:01 |
|* 2 | TABLE ACCESS STORAGE FULL | T1 | 2 | 22 | 9 (0)| 00:00:01 |
| 3 | TABLE ACCESS BY INDEX ROWID| T2 | 10 | 650 | 1 (0)| 00:00:01 |
|* 4 | INDEX UNIQUE SCAN | T2_IDX_01 | 1 | | 0 (0)| 00:00:01 |
------------------------------------------------------------------------------------------
The case for the Siebel query was little more complex but ulitmately it was the magic number 82 that caused the optimizer to choose a inefficient join order.